Equação de 2º grau

Álgebra Linear - Equação de 2º grau

Equação de 2º grau, diferente da equação de 1º grau, possui duas raízes (duas incógnitas) e normalmente aparece na seguinte forma:

ax²+bx+c=0

Para resolvermos esta equação utilizamos a fórmula de Bhaskara.

Se lê, X é igual menos B, mais ou menos raiz quadrada de Delta, dividido por duas vezes A. Os sinais de mais ou menos na equação é o que distinguiram as duas raízes.

Exemplo 1:

x²-5x+6=0 que é o mesmo que 1x²-5x+6=0, apenas ocultamos o número 1 para deixar a equação com uma melhor visualização, já que o 1 é o elemento neutro da multiplicação.

Neste caso devemos organizar os valores para iniciar a resolução da equação.

ax²+bx+c=0

x²-5x+6=0

(1)x²+(-5)x+(6)=0

a=1, b=-5 e c=6

Já encontramos e organizamos os valores de a, b e c. Agora vamos calcular o valor de Delta (▲).

Utilizando a fórmula de Bhaskara, temos:

▲= b²-4.a.c

▲= (-5)²-4.(1).(6)

▲=25-24

▲=1

Agora vamos realizar a segunda etapa da resolução, substituindo as letras da fórmula pelos valores encontrados.

Como foi explicado no início da matéria, a equação de 2º grau possui normalmente duas raízes, neste caso vamos chama-las de x¹ e x² e para distinguir as duas raízes vamos separar o sinal de mais do sinal de menos.

x¹= 5+1/2 

x¹=3

x²= 5-1/2

x²=2

O conjunto solução da equação é:

S={3,2} 

Exemplo 2:

5x²-2x+10=0

a=5

b=-2

c=10

▲= b²-4.a.c

▲= (-2)²-4.(5).(10)

▲=4-200

▲=-196

Neste caso, o valor de Delta (▲) é negativo, sendo assim, a equação não possui raízes reais e encerramos a equação já nesta etapa.

Exemplo 3:

-x²-4x-4=0

a=-1

b=-4

c=-4

▲= b²-4.a.c

▲= (-4)²-4.(-1).(-4)

▲=16-16

▲=0

No caso de Delta (▲) ser igual a 0, a resolução será da mesma maneira, porém, notaremos que a equação possuirá apenas uma raiz.

x¹= 4+0/-2

x¹= -2

x²= 4-0/-2

x²= -2

S={-2}

Equação incompleta

Equação incompleta é toda equação que não possui os valores de b ou c, porém, ainda assim continua sendo uma equação de 2º grau e deve utilizar a mesma resolução, com o detalhe de que deve utilizar o valor 0.

Exemplos:

-x²-8=0

Não possui o valor 'bx', neste caso b=0

2x²+4x=0

Não possui um valor para 'c', neste caso c=0

5x²=0

Não possui o valor para 'bx' e 'c', neste caso b=0 e c=0.

Relação entre raízes.

A soma e o produto da raízes da equação (x1 e x2) possui uma relação que é dada pela seguinte fórmula.

Exercício:

Na equação x²+bx+c=0 , suas raízes possuem os seguintes valores x1=1 e x2=3. Descubra qual é o valor de b e c.

Resolução:

O enunciado fornece 3 informações importantes.

x1=1

x2=3

Como não aparece a incógnita 'a' na fórmula, é certo que a=1

a=1

x1+x2=-b/a

1+3=-b/1

-b=4

b=-4

x1.x2=c/a

1.3=c/1

c=3

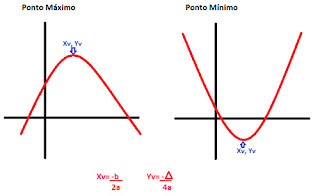
Ponto Máximo e Ponto Mínimo da Parábola (Vértice)

O Ponto Máximo (a<0) ou Ponto Mínimo (a>0) é o valor do ponto do eixo 'x' no vértice da parábola. Dado pela equação:

O Valor Máximo (a<0) ou Valor Mínimo (a>) é o valor do ponto do eixo 'y' no vértice da parábola. Dado pela equação:

Exercício: Qual é o ponto máximo ou mínimo da parábola na seguinte equação: x²+2.x-3=0

a=1

b=2

c=-3

Como a>0, iremos encontrar o ponto e valor mínimo.

Δ =(2)² - 4.1.(-3)

Δ = 4+12

Δ = 16

Xv= -b/2.a

Xv= -2/2

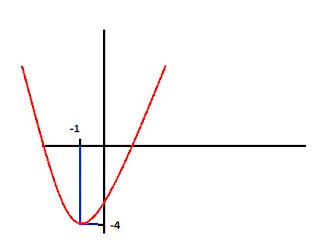
Xv=-1

Yv= -Delta/4.a

Yv= -16/4

Yv= -4