Fios Ideais

Fios Ideais

Fio ideal se caracteriza por ter sua massa desprezível e ser capaz de transmitir toda força que nele é aplica entre as extremidades.
 A força que exercemos em um fio ideal sempre será de tração, esta força tem a mesma direção do fio e a intensidade dessa força será igual em ambas as extremidades.

Agora vamos esclarecer algumas regras sobre seno e co-seno.

Não vou entrar em detalhes sobre seno e co-seno, mas gostaria de fazer uma breve observação sobre estas funções trigonométricas.

Quando observamos ambos em um plano cartesiano, observamos que o valor do seno esta diretamente ligado ao eixo Y (ordenadas) e o co-seno ao eixo X (abcissas).

Quando o seno ou co-seno estão em seu ponto mais alto do plano cartesiano, seu valor será 1 e no ponto mais baixo o valor será 0.

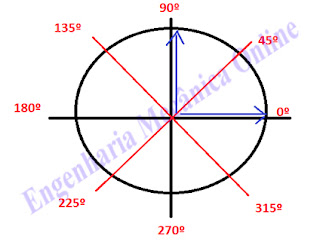
Vamos observar nesta figura:

Compare os valores da tabela, no ângulo de 0º, o eixo Y está em no seu valor mínimo (0), já o eixo X está no seu valor máximo (1). Quanto mais ao centro do plano cartesiano, menor será o valor.

No ângulo de 45º, podemos observar um equilíbrio entre seno e co-seno, ambos valem 0,707.

Já no ângulo de 90º o eixo Y possui seu valor máximo (1) e o eixo X o mínimo (0).

Vamos realizar alguns exercícios baseados neste conceito:

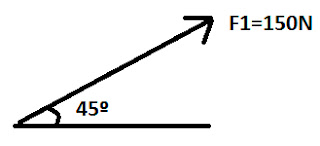
1) Represente as forças i(F) na forma cartesiana, ou seja, determine Fx e Fy.

Sabemos que F1 possui 150N de força e queremos qual o valor dessa força para o eixo X e Y em um ângulo de 45º.

Lembrando que o seno está vinculado ao eixo Y e o co-seno ao eixo X.

Para calcular Fx, multiplicamos F1 pelo co-seno de 45º.

Força do eixo X:

Fx= F1.Cos45º

Fx= 150N.0,707

Fx= 106,06N

Para calcular Fy, multiplicamos F1 pelo seno de 45º.

Força do eixo Y:

Fy= F1.Sen45º

Fy= 150N.0,707

Fy= 106,06N

Observamos que há um equilíbrio de forças no ângulo de 45º, ambos os eixos cartesianos possuem aproximadamente 70% da força original (F1).

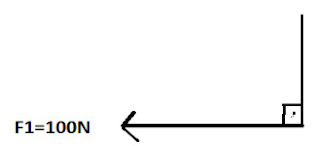
2) Encontre Fx e Fy.

Neste exercício obedeceremos o plano cartesiano e podemos observar que F1 está em um ângulo de 180º e não em um ângulo de 0º ou 90º.

Fx= F1.Cos180º

Fx= 100N.(-1)

Fx= -100N

Fy= F1.Sen180º

Fy= F1.0

Fy= 0