Coeficiente Angular da Reta

Dois pontos distintos do plano cartesiano P(x1, y1) e Q(x2,y2), formam uma reta não vertical chamada r, sendo que esta reta forma um ângulo de inclinação 'α' ao cruzar com o eixo 0x.

Chamamos de M o coeficiente angular da reta 'r', dado pela equação:

M=(y2-y1)/(x2-x1)

Exemplo: Determine o coeficiente andular da reta 'r' que passa pelos pontos P(1,2) e Q(3,4).

P(x1,y1)

Q(x2,y2)

M=4-2/3-1

M=2/2

M=1

Equação da reta

Considere P(xo,yo) e Q(x,y), pontos distintos da reta 'r', neste caso vamos descobrir como encontrar a equação reduzida da reta.

P(x1,y1)

 P(xo,yo)

Q(x2,y2)

Q(x,y)

M=(y2-y1)/(x2-x1)

M=(y-yo)/(x-xo)

(y-yo)=M.(x-xo)

Para menorizar esta formula pronunciamos assim:"ioiô m xoxô".

A equação (y-yo)=M.(x-xo) é a equação da reta 'r' de coeficiente angular M que passa pelo ponto Po.

Exemplo: Considere os pontos da reta 'r' P(1,2) e Q(4,-1). Determine o coeficiente angular da reta e a equação da reta 'r'. Esboce o gráfico.

Coeficiente angular da reta

M=(y2-y1)/(x2-x1)

M=(-1-2)/(4-1)

M=-3/3

M=-1

Equação da reta

(y-yo)=M.(x-xo)

Para encontrar a equação da reta podemos escolher qualquer um dos pontos da reta P ou Q, o resultado será o mesmo. Neste caso vou usar o ponto P(1,2).

(y-2)=-1.(x-1)

y-2=-x+1

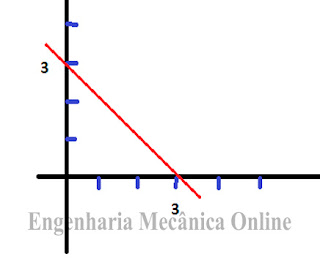
y=-x+3

Gráfico:

Dica: 

Quando o coeficiente angular for < 0, a reta será decrescente ( \ ).

Quando o coeficiente angular for > 0, a reta será crescente ( / ). 

Para o coeficiente = 0, será uma reta paralela ao eixo x ( - ).

Agora tente realizar este exercícios sobre a matéria, em caso de dúvida envie sua dúvida por comentário.

Calcule o coeficiente angular e a equação da reta pelos pares de pontos e faça os respectivos gráficos.

a) (-2,0) e (0,2)

b) (-3.5) e (-2,7)

c) (-1,1) e (1,-2)

d) (-1,1) e (-3,2)