Integral - Teoria
Integral possui inúmeras aplicações práticas, as principais são a possibilidade de realizar cálculos com curvas, determinar a área sob uma curva, volume de objetos curvos, pressão exercida em objetos curvos. Área Uma das aplicações do cálculo integral é a determinação de uma área sob uma curva, a qual daremos um maior foco, onde obtemos uma função f(x).
Para ilustrar a teoria do cálculo da integral vamos exemplificar da seguinte forma:
Porém ainda há espaços que não foram preenchidos pelo retângulo, então será um cálculo muito impreciso. Mas e se aumentarmos o número de retângulos dentro da área sob a curva.
Dois retângulos
Quatro retângulos
Oito retângulos
Como podemos notar, quanto mais retângulos desenhamos mais preciso será o cálculo da área, então enquanto o número de retângulo (n) tende ao infinito mais fiel será o resultado.
Dividindo o intervalo [A, B] em n intervalos de comprimento temos: Δx= (b-a)/n.
Tome xi* ∈ [xi-1, xi] pontos arbitrários, onde i= 1, 2,..., n.
Cada retângulo Ri tem área dada pela seguinte equação:
A equação da soma de todos os retângulos é dada por:
Portanto, a área sob o gráfico de f é dada pela equação:
Concluindo que , a equação da integral da função definida por f na intervalo [A, B] é:
Exemplo de fixação
Use retângulos para estimar a área sob a parábola y=x² no intervalo de 0 à 1 do eixo x. Use apenas 4 retângulos.
Limite dos intervalos à esquerda:
Limite dos intervalos à direita:
Portando a área sob a curva está entre o intervalo 0,21875 < A < 0,46875, se aumentarmos a quantidade de retângulo vamos observar que este intervalo se aproxima do valor real da área. Observe a tabela abaixo:
Resposta: A área do a curva é de 0,333333 unidades².







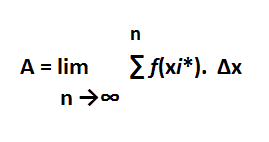








Nenhum comentário:
Postar um comentário
Deixe aqui seu comentário, dica, crítica, dúvida ou sugestão.